The Offspring Selection Genetic Algorithm (OSGA) is an evolutionary optimization method that refines a population of solutions (like expression trees) over successive generations. Its core principle lies in its selective acceptance of offspring: after parent solutions generate new offspring through recombination and mutation, only those offspring whose “suitability” exceeds a dynamically adjusting threshold are allowed to join the next generation. This threshold, combined with an adaptive difficulty setting, progressively raises the bar for acceptance, effectively “steering” the population towards increasingly better solutions. An elite pool continuously preserves the very best solutions found throughout the process, ensuring overall progress until a predefined termination condition is met.
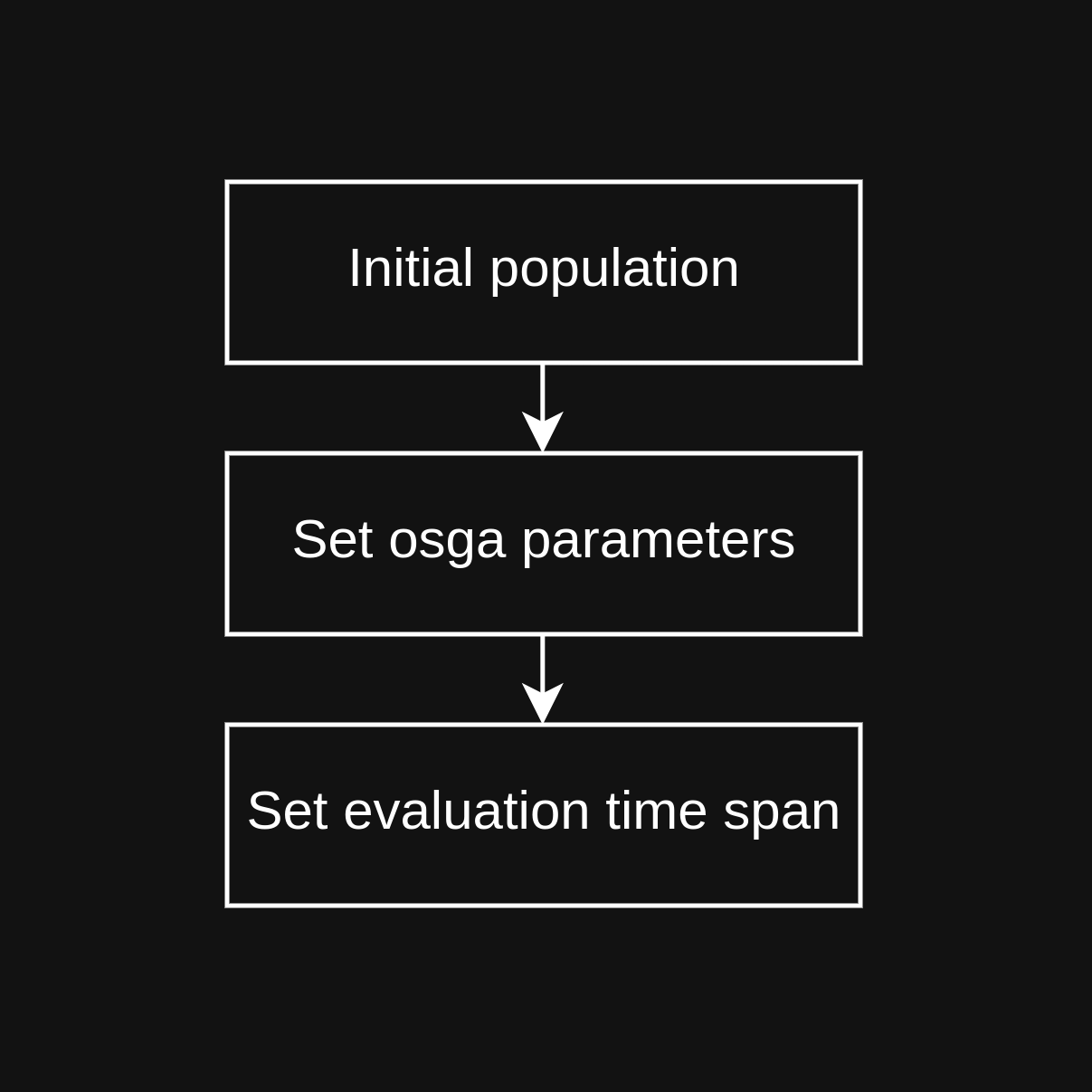
OSGA Begin Phase
First, the algorithm attempts to load existing expression trees from a specified directory. These pre-existing trees form the initial pool of candidate solutions. If the number of loaded trees is less than the target initial population size for the OSGA, the remaining slots are filled with newly generated, random expression trees. This ensures a complete starting group for the evolutionary process. Simultaneously, various parameters governing the OSGA’s behavior are configured. These include settings like the target population size, the maximum number of generations, the target selection pressure limit, and specific parameters for selecton, crossover and mutation.
OSGA
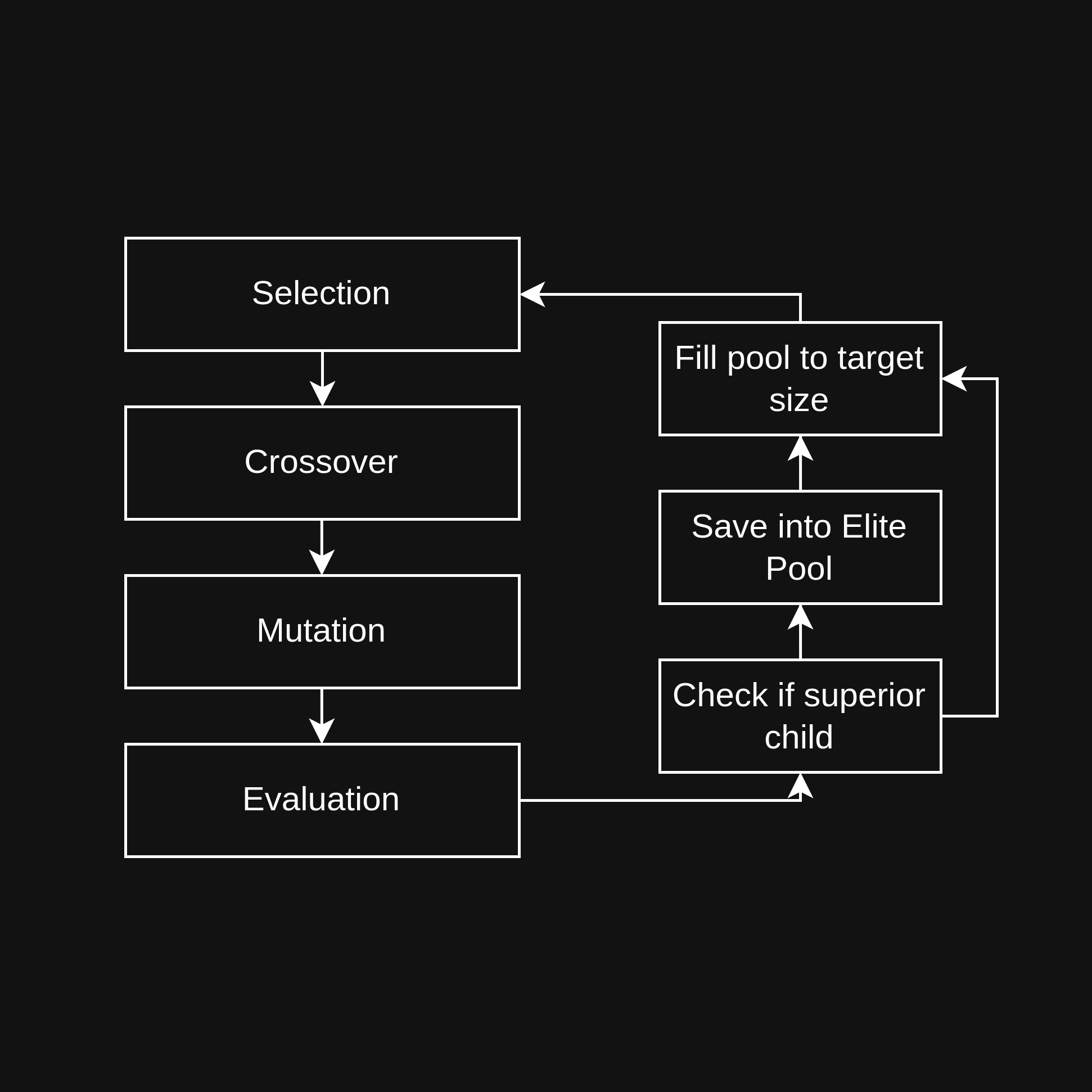
In each generation, parent solutions are selected and then produce two offspring through recombination (crossover). These offspring subsequently undergo modification (mutation). Each offspring’s suitability is then evaluated. An offspring is accepted into the next generation if its suitability surpasses a dynamic threshold, determined by the parents’ suitability and an adaptive difficulty setting. Accepted offspring go to the “good children pool,” while others enter a “bad children pool.”
Following this, the observed selection pressure (ratio of accepted offspring to group size) is calculated, and the difficulty setting is increased to raise the bar for future acceptance. The next generation is then filled to its target size, prioritizing accepted offspring, then those from the “bad children pool,” followed by remaining current group members, and finally, new random solutions if necessary.
Throughout this process, an “elite pool” consistently tracks and preserves the best solutions found so far. These elites are regularly incorporated into the succeeding generation, ensuring top performers remain part of the evolving group. Suitability data is recorded for each generation. The algorithm continuously checks for termination criteria (e.g., max generations, target selection pressure); once met, this phase concludes.

OSGA End Phase
Once the termination conditions are met, the accumulated suitability history (recorded throughout the OSGA Execution Phase) is written to a data file, providing a comprehensive record of the evolutionary process. All the evolved expression trees from the final generation, or specifically from the elite pool, are saved to a designated directory. Crucially, the single best-performing expression tree from the entire evolutionary run (typically the top elite solution) is identified and specifically marked. This “best tree” is intended for subsequent use, such as for the inverter application mentioned in the context. Finally, the algorithm returns the final, evolved group of solutions (e.g., the final generation or the elite pool), ready for further analysis or deployment.
Selection
To create the next generation of expression trees out of the current tree pool, at first, suited parent trees for reproduction need to be selected. For this purpose, different selection algorithms can be used.
One might think the best idea would be to take the fittest parents for reproduction. But this strategy is not very well suited for finding the globally best performing tree.
Two of the possible algorithms are random selection and tournament selection. While random selection works independantly of the fitness (as the name suggests), tournament-selection selects the fittest tree out of a random subgroup. The size of the subgroup is a parameter of the algorithm.
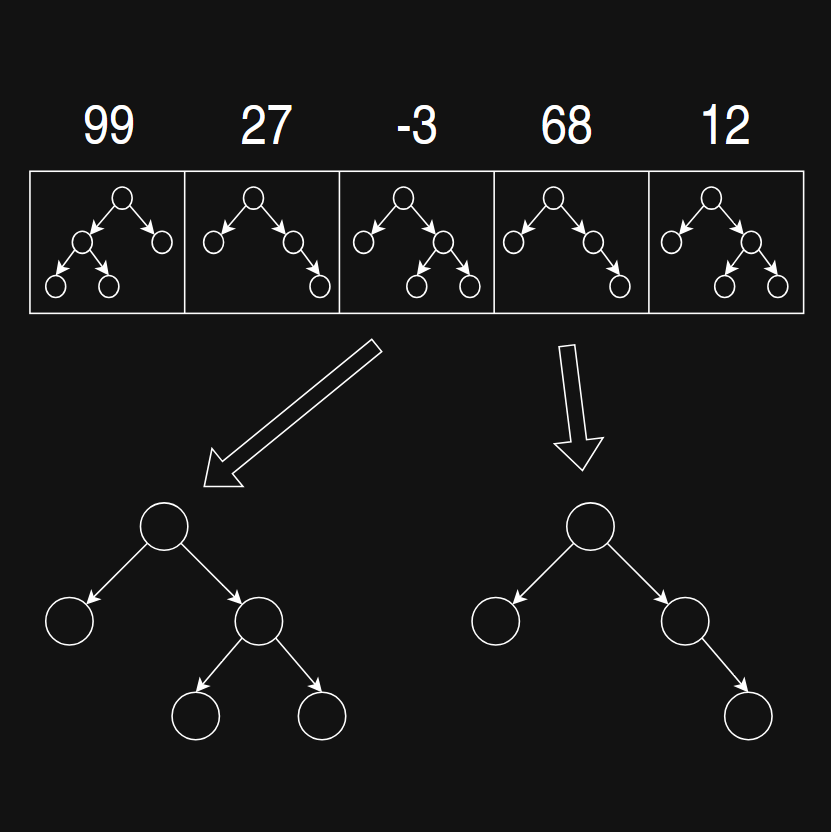
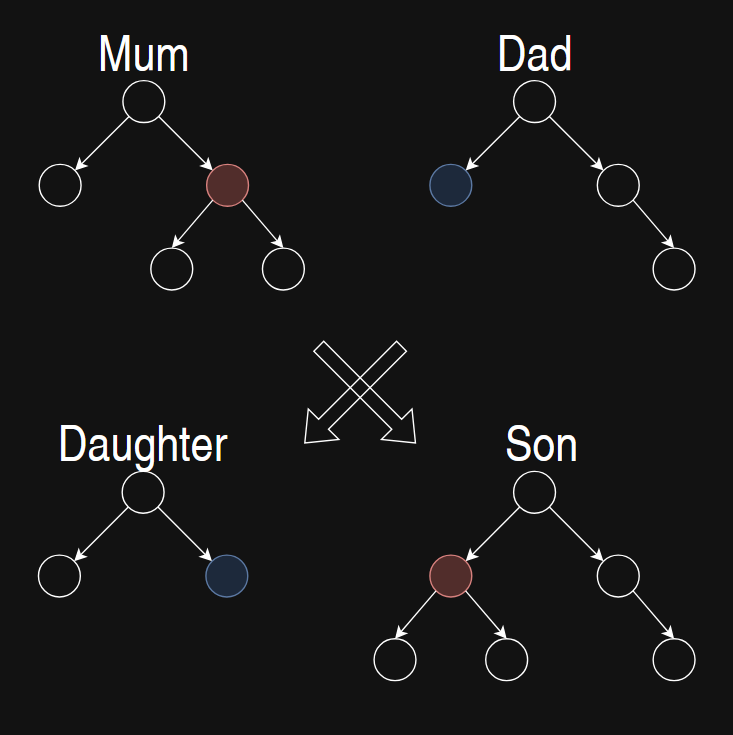
Crossover
After the parent trees have been selected, it is time for the actual reproduction process. To generate the offspring trees, crossover algorithms are used. Their goal is to combine the good performing characteristics of the parent trees, and create even better performing children.
There are many possible ways to implement the crossover. The one we use firstly copies the parent trees. Then each tree randomly chooses one node. After these two nodes get swapped, the new generation is born.
Mutation
Before the freshly born generation gets evaluated, some of the new expression trees should be changed a bit. This mutation process helps the algorithm finding a global optimal formula.
The goal is to give the new generation the possibility of creating new well-working patterns, which their parents weren’t able to find out. Therefore different mutation functions can be used:
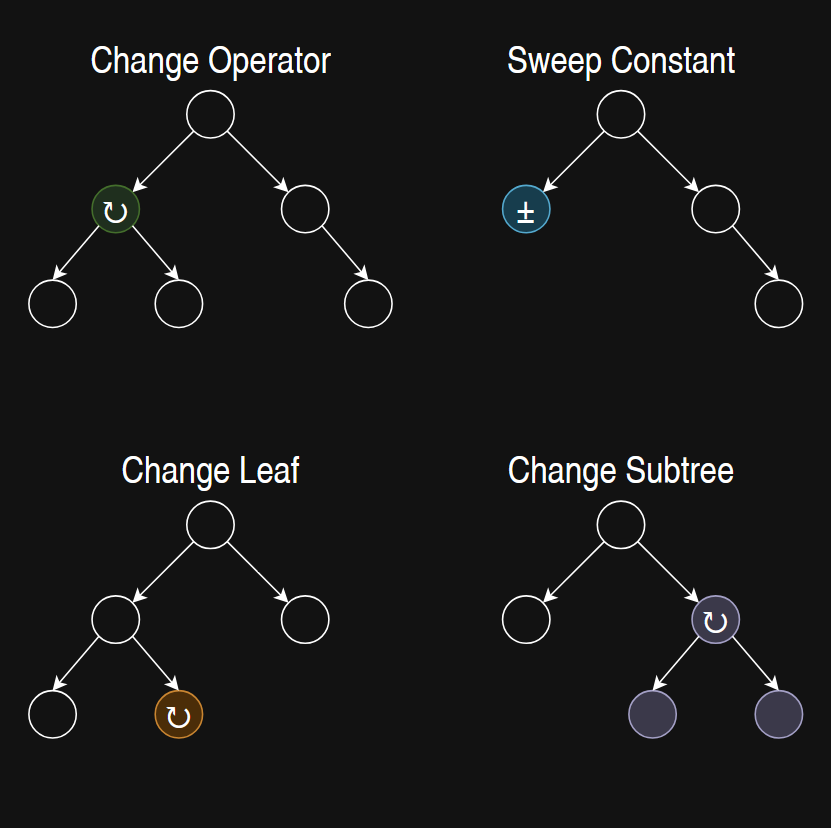
- Change Operator:
Swap out a randomly chosen operator with a randomly created operator. - Sweep Constant:
Change the value of a constant leaf randomly but in relation to its original value. - Change Leaf:
Swap out a randomly chosen leaf with a randomly created leaf. Both chosen and created one can either be a constant or a variable. - Change Subtree:
Select a completly random node and swap it with a randomly created tree.
In our algorithm the combination of all mutation functions are used. Each tree performs each mutation function a certain amount of times and with a certain probability. These values are part of the hyper parameters.